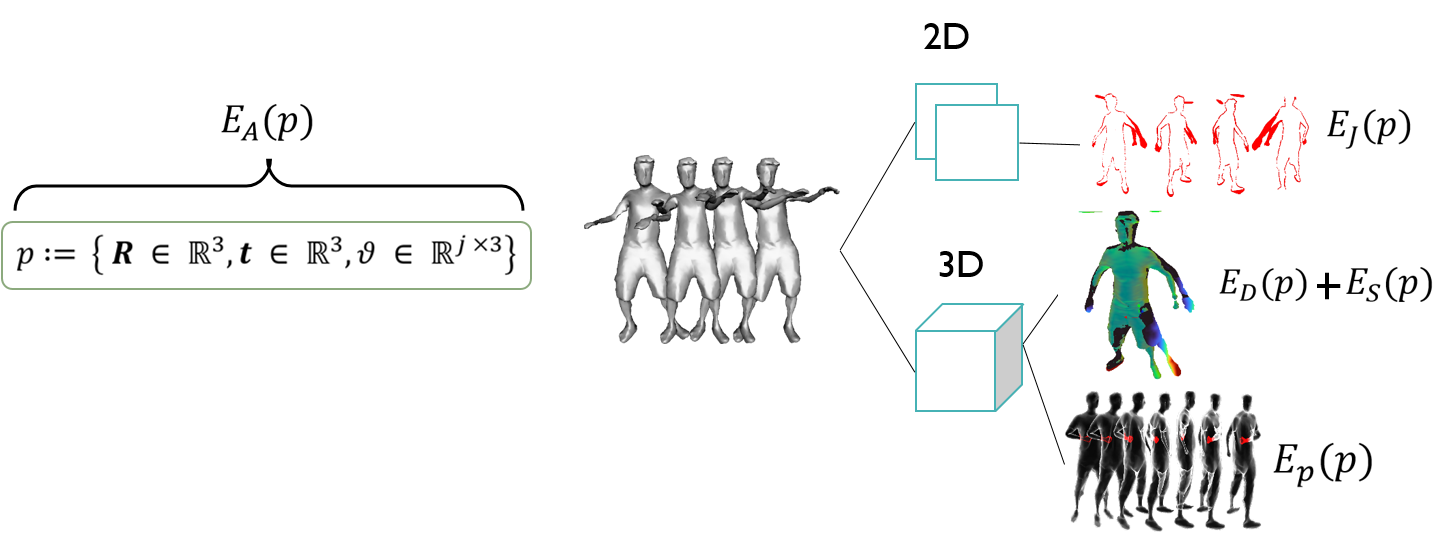
Objective Function

The objective function of each experiment is a weighted linear combination of five individual error terms:

$E(\mathbf{p})= \lambda_J E_J(\mathbf{p}) + \lambda_D E_D(\mathbf{p}) + \lambda_S E_S(\mathbf{p}) + \lambda_P E_P(\mathbf{p}) +\lambda_A E_A(\mathbf{p}),$

where $\mathbf{p}$ denote the unknown variables, which in our case are the pose parameters that animate the template mesh into a specific pose in order to fit into the current live data. The different error terms are:

an extrapolated 3D Chamfer distance metric, $E_D$
a surface alignment matching term, $E_S$
a penalization term of mesh self-intersections, $E_P$
the 2D projective silhouette error, $E_J$
an anthropometric penalization of unnatural human poses, $E_A$

These can be categorized with respect to their domain:

$3D$	$2D$	Pose
Chamfer distance ( $E_D$ )	Silhouette error ( $E_J$ )	Anthropometric prior ( $E_A$ )
Surface alignment( $E_S$ )
Self-penetration error ( $E_P$ )

or a data fitting perspective:

Data Terms	Constraints
Chamfer distance ( $E_D$ )	Self-penetration error ( $E_P$ )
Surface alignment ( $E_S$ )	Anthropometric prior ( $E_A$ )
Silhouette error ( $E_J$ )

Our complete objective as formulated above is a linear weighted combination of these terms as weighted by the respective weights $\lambda$ . More details can be found in [6].

Each pose parameter vector $\mathbf{p}:=\{\mathbf{R},\mathbf{t},\boldsymbol{\theta}\}$ , corresponds to a global root rotation $\mathbf{R}\in\mathbb{R}^3$ and translation $\mathbf{t}\in\mathbb{R}^3$ , as well as per joint $j\in[1, J]$ rotation parameters $\boldsymbol{\theta}\in\mathbb{R}^{h\times3}$ for all joints $J$ ,parameterized by their exponential map [1]. All template meshes are automatically skinned and rigged with [2]. By animating the rigged and skinned template with the pose parameters $\mathbf{p}$ we get a re-posed mesh of the template $\mathbf{\hat{V},\hat{N}}=DQS(\mathbf{V},\mathbf{N},\mathbf{p})$ , with $\mathbf{\hat{V}}$ and $\mathbf{\hat{N}}$ the template’s vertices and normals respectively (connectivity, i.e. triangles/faces remain consistent). For animation we use dual quaternion skinning (DQS) [3].

Four error functions are formulated indirectly to the optimized variables through the animated mesh, while the anthropometric prior $E_A$ is calculated solely on the pose parameters $\mathbf{p}$ .

Regarding the former, we first calculate the Euclidean Distance Transform (EDT) using a separable Chamfer implementation [4] defined on a voxel grid $\mathbf{G}$ whose bounding box is tightly calculated using the input live data. Thus our $3D$ error terms are defined:

$E_D=\frac{1}{V}\sum_{\mathbf{v}\in\mathbf{\hat{V}}}\mathcal{S}_\mathbf{P}(\mathbf{G},\lfloor\mathbf{v}\rfloor)+||\mathbf{v}-\lfloor\mathbf{v}\rfloor||_2$
where a sampling operation $\mathcal{S}$ defined on the EDT grid, samples the distance at each animated vertex $\mathbf{v}$ , clamped within the confines of the bounding box that the EDT was calculated in through $\lfloor . \rfloor$ . Given that pose parameters $\mathbf{p}$ may be explored outside the bounding box that the EDT is defined in, we further supplement the sampled distance, with an approximate distance that is negligible within the bounding box, but allows the error to extrapolate outside its bounds and offer meaningful evaluations.
$E_S=\frac{1}{V}\sum_{(\mathbf{v},\mathbf{n})\in(\mathbf{\hat{V}},\mathbf{\hat{N}})}1-\langle\nabla\mathcal{S}_{\mathbf{P}}(\mathbf{G},\mathbf{\lfloor\!v\rfloor}),\mathbf{n}\rangle^2$
which represents a surface alignment error using the gradient of the distance field and the animated template’s surface normals (an adaptation of [4]). Both $E_D$ and $E_S$ provide a combined animated-to-live distance.
$E_P=\sum_{\mathbf{v_q}\in\mathbf{\hat{V}^{q}}}\sum_{j \in \mathbf{J}}\prod_{a}\epsilon_a(\mathbf{v}_q,\mathbf{T}_j),$
which enforces a penalization of unnatural poses (body parts being inside, i.e. penetrating, other body parts). We use a coarse proxy of the template to avoid excessive computational costs, with $\epsilon$ being a binary function that tests whether the query vertex $\mathbf{v}_q$ is inside the body part proxy shape.

Finally, we also employ a projective $2D$ error:

$E_J(\mathbf{p})=\frac{1}{K}\sum_k^K1-\frac{\mathbf{M}^P_k\cap\mathbf{M}^A_k}{\mathbf{M}^P_k\cup\mathbf{M}^A_k}$
which represents a Jaccard metric of (dis-)similarity, otherwise known as intersection-over-union (IoU) [5]. This is defined after rendering the silhouette images of the live $\mathbf{M}^P_k$ and animated meshes $\mathbf{M}^A_k$ at each $k\in K$ input viewpoints. This error offers an approximate notion of the live-to-animated distance.

The overall error calculation process for each input pose parameters is depicted below:

Errors

[1] Grassia, F. S. (1998). Practical parameterization of rotations using the exponential map. Journal of graphics tools, 3(3), 29-48.

[2] Baran, I., & Popović, J. (2007). Automatic rigging and animation of 3d characters. ACM Transactions on graphics (TOG), 26(3), 72-es.

[3] Kavan, L., Collins, S., Žára, J., & O’Sullivan, C. (2007, April). Skinning with dual quaternions. In Proceedings of the 2007 symposium on Interactive 3D graphics and games (pp. 39-46).

[4] Coeurjolly, D., & Montanvert, A. (2007). Optimal separable algorithms to compute the reverse euclidean distance transformation and discrete medial axis in arbitrary dimension. IEEE transactions on pattern analysis and machine intelligence, 29(3), 437-448.

[4] Smirnov, D., Fisher, M., Kim, V. G., Zhang, R., & Solomon, J. (2020). Deep parametric shape predictions using distance fields. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 561-570).

[5] Jaccard, P. (1901). Distribution de la flore alpine dans le bassin des Dranses et dans quelques régions voisines. Bull Soc Vaudoise Sci Nat, 37, 241-272.

[6] To appear.