Abstract

Omnidirectional vision is becoming increasingly relevant as more efficient 360^o image acquisition is now possible. However, the lack of annotated 360^o datasets has hindered the application of deep learning techniques on spherical content. This is further exaggerated on tasks where ground truth acquisition is difficult, such as monocular surface estimation. While recent research approaches on the 2D domain overcome this challenge by relying on generating normals from depth cues using RGB-D sensors, this is very difficult to apply on the spherical domain. In this work, we address the unavailability of sufficient 360^o ground truth normal data, by leveraging existing 3D datasets and remodelling them via rendering. We present a dataset of 360^o images of indoor spaces with their corresponding ground truth surface normal, and train a deep convolutional neural network (CNN) on the task of monocular 360^o surface estimation. We achieve this by minimizing a novel angular loss function defined on the hyper-sphere using simple quaternion algebra. We put an effort to appropriately compare with other state of the art methods trained on planar datasets and finally, present the practical applicability of our trained model on a spherical image re-lighting task using completely unseen data by qualitatively showing the promising generalization ability of our dataset and model.

Angular Loss on the Hyper-Sphere

According to Euler's rotation theorem, a transformation of a fixed point $ \textbf{p}(p_x, p_y, p_z) $ can be expressed as a rotation given by an angle $ \theta $ around a fixed axis $ \textbf{u}(x, y, z) = x\hat{\textbf{i}} + y\hat{\textbf{j}} + z\hat{\textbf{k}} $, that runs through $ \textbf{p} $. This kind of rotation can be easily represented by a unit quaternion $ \textbf{q}(w, x, y, z) $.

Therefore, we can represent two normal vectors $ \hat{\textbf{n}}_1(n_{1_x},n_{1_y},n_{1_z}) $ and $ \hat{\textbf{n}_2}(n_{2_x},n_{2_y},n_{2_z}) $ as the pure quaternions $ \textbf{q}_1(0, n_{1_x},n_{1_y},n_{1_z}) $ and $ \textbf{q}_2(0, n_{2_x},n_{2_y},n_{2_z}) $ respectively. Then their angular difference can be expressed by their transition quaternion [ref], which represents a rotation from $ \textbf{n}_1 $ to $ \textbf{n}_2 $:

$$\begin{align*} \textbf{t} = \textbf{q}_1 \textbf{q}_2^{-1} \end{align*}$$

Because $ \textbf{q}_1 $ and $ \textbf{q}_2 $ are unit quaternions: $ \textbf{q}^{-1} = \textbf{q}^* $, where $ \textbf{q}^* $ is the conjugate quaternion of $ \textbf{q} $.

In addition, because $ \textbf{q}_1 $ and $ \textbf{q}_2 $ are pure quaternions: $ \textbf{q}^{*} = -\textbf{q} $, and:

$$\begin{align*} \textbf{q}_1 \textbf{q}_2 = \textbf{q}_1 \cdot \textbf{q}_2 - \textbf{q}_1 \times \textbf{q}_2 \end{align*}$$

Finally, the rotation angle of the transition quaternion (and therefore the angular difference between $ \textbf{n}_1 $ and $ \textbf{n}_2 $ is calculated by the inverse tangent between the real and the imaginary parts of the transition quaternion, which are reduced to their dot and cross product, due to being unit, pure quaternions:

$$\begin{align*} tan(\theta) = \frac{\vert\vert\textbf{q}_1 \times \textbf{q}_2\vert\vert}{\textbf{q}_1 \cdot \textbf{q}_2} \Rightarrow \\ \theta = atan(\frac{\vert\vert\textbf{q}_1 \times \textbf{q}_2\vert\vert}{\textbf{q}_1 \cdot \textbf{q}_2}) \end{align*}$$

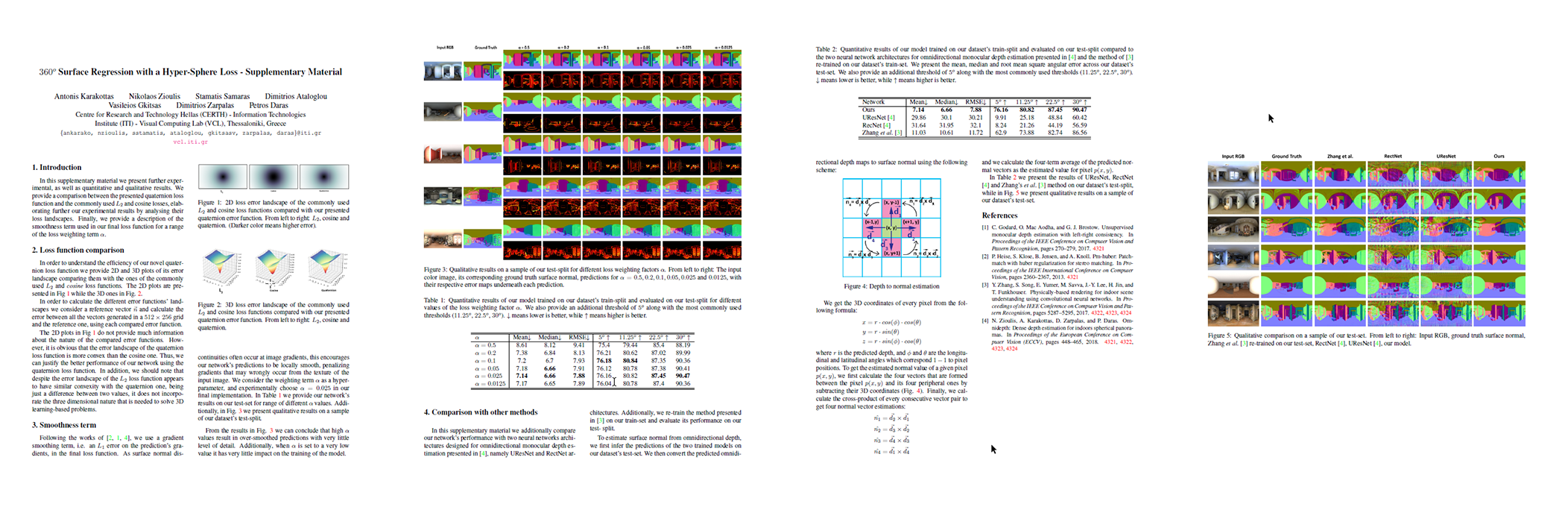
Quantitative Results using different Loss functions

Loss Functions	Mean	Median	RMSE	5o	11.25o	22.5o	30o
L2	7.72	7.23	8.39	73.55	79.88	87.72	90.43
Cosine	7.63	7.14	8.31	73.89	80.04	87.29	90.48
Hyper-Sphere	7.24	6.72	7.98	75.8	80.59	87.3	90.37
Hyper-Sphere + Smoothness	7.14	6.66	7.88	76.16	80.82	87.45	90.47

Loss Landscapes

Data

The 360^o data used to train our model are available here and are part of a larger dataset [1,2], which is composed of color images, depth, and surface normal maps for each viewpoint in a trinocular setup.

Code

Our training and testing code that can be used to reproduce our experiments can be found at the corresponding Github repository.

• train.py for model training .
• test.py for testing a trained model.
• infer.py for infering a pre-trained model's prediction on a single image.

In order to train and test our model we use settings files in .json format. Template settings files for training and testing can be found here.

Pre-trained model

Our PyTorch pre-trained weights (trained for 50 epochs) are released here.

Publication

Paper

Supplementary

Citation

    
      @inproceedings{karakottas2019360surface,
        author      = "Karakottas, Antonis and Zioulis, Nikolaos and Samaras, Stamatis and Ataloglou, Dimitrios and Gkitsas, Vasileios and Zarpalas, Dimitrios and Daras, Petros",
        title       = "360 Surface Regression with a Hyper-Sphere Loss",
        booktitle   = "International Conference on 3D Vision",
        month       = "September",
        year        = "2019"
      }
    
   

Acknowledgements

We thank the anonymous reviewers for their helpful comments.

The project has received funding from the European Union's Horizon 2020 research and innovation programme Hyper360 under grant agreement No. 761934.

We would like to thank NVIDIA for supporting our research with the donation of an NVIDIA Titan Xp GPU through the NVIDIA GPU Grant Program.

References

[1] Zioulis, N., Karakottas, A., Zarpalas, D., Daras, P., (2018). Omnidepth: Dense depth estimation for indoors spherical panoramas. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 448-465).